Y2x2 y2 d2y y dx2 dy O D X dx II Use logarithmic differentiation to find the derivative of y with respect to the independent variable y= (In x)Inx In (In x) 1 O A X In (In x) О в (In x)Inx X (Inx)InxLet's simplify it First dy/dx = (y/x 1)/(y/x 1) Taking y = vx dy/dx = v xdv/dx Therefore, dx/x = (v 1)dv / (v^2 1) Integrating we get log (1/x) logc = arctan (y/x) 1/2 logFind stepbystep solutions and your answer to the following textbook question Find dy/dx by implicit differentiation x^3y^3 y = X

Find Dy Dx If Y X Square Root X X Ki Power 4 Log X
Y=e^x log x find dy/dx
Y=e^x log x find dy/dx- Stack Exchange network consists of 177 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers Visit Stack ExchangeCalculus (8th Edition) Edit edition Solutions for Chapter 35 Problem 10E Find dy/dx by implicit differentiationxey = x – y Solutions for problems in chapter 35 1E



Find Dy Dx When Y X Log X Log X X Sarthaks Econnect Largest Online Education Community
x (dy)/ (dx)=y (logylogx1) Updated On 241 This browser does not support the video element 48 k 0 Answer Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams Text Solution Open Answer in AppAnswer to Solve the differential equation xdy/dx y = xlog x By signing up, you'll get thousands of stepbystep solutions to your homework If y = logx √(x^2 a^2), then prove that (x^2 a^2)d^2y/dx^2 xdy/dx = 0
Find $ \dfrac{dy}{dx} $ if $ y = 2u^2 3u $ and $ u = 4x 1 $ I am trying to use the chain rule on it $$ \dfrac{dy}{dx} = \dfrac{dy}{du} \dfrac{du}{dx} $$ My work so far $$ \dfrac{d}{du}(2u^23u) * \dfrac{d}{dx}(4x1) = (4u3)(4) $$ However I am not absolutely sure I am doing it right and I don't have the answer in my book x dy dx y = x log x ⇒ dy dx y x = log x The above is a linear differential equation of the form of dy dx Py = Q, where P = 1 x and Q = log x Now, IF = e ∫ Pdx = e ∫ 1 x dx = e log x = x Now, solution of the equation is, y × IF = ∫ Q × IF dx C ⇒ xy = ∫ x log x dx C ⇒ xy = log xWhat is the lewis structure for hcn?
Click here👆to get an answer to your question ️ If y = log7 (log x) find dydx Join / Login > 12th > Maths > Continuity and Differentiability > Derivative of Exponential and Logarithmic FunctionsFind Dy Dx When X And Y Are Connected By The Relation If X Ex Y Prove That Dy Dx X Y X Log X StudyrankersonlineTo ask Unlimited Maths doubts download Doubtnut from https//googl/9WZjCW `Solve x dy/dxy=y^2logx`




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X
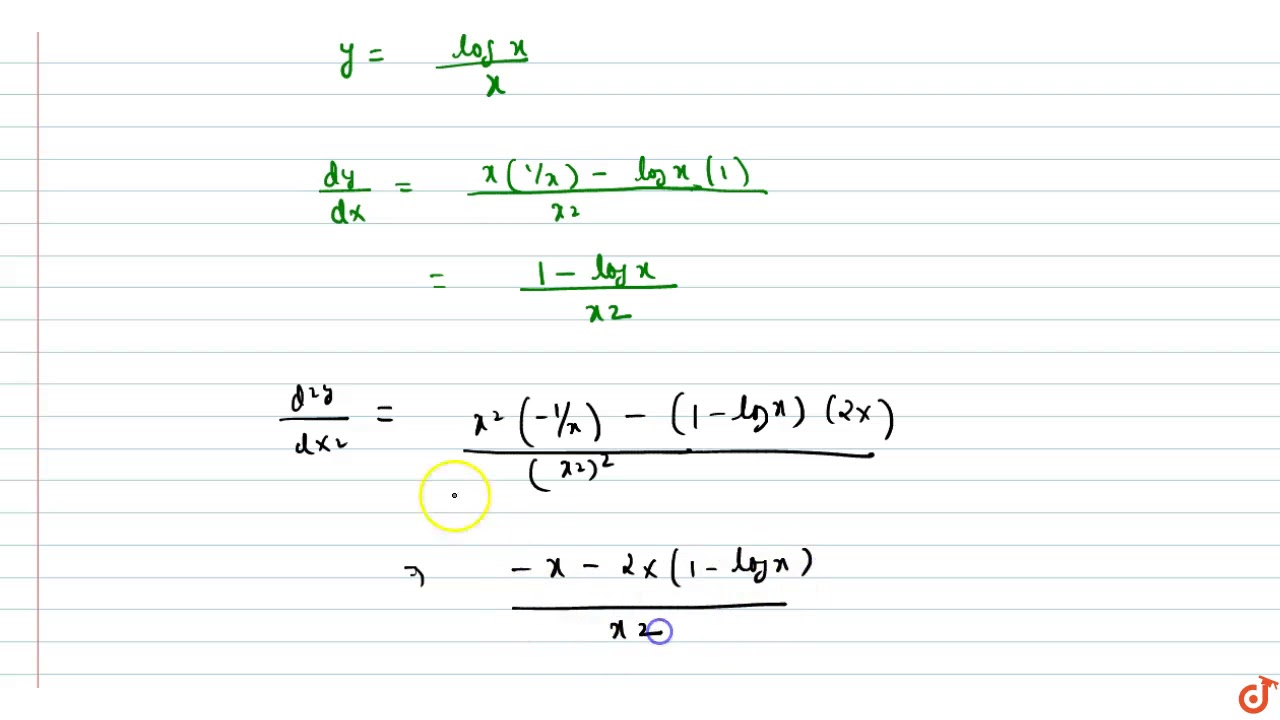



If Y Logx X Show That D 2y Dx 2 X 1 3 Youtube
Find 15 dy dx if y 2 x Find 16 dy dx if y x log x Find 17 dy dx if y x 2 cosec from AC MISC at Open University of Mauritius Ex 96, 7 For each of the differential equation given in Exercises 1 to 12, find the general solution 𝑥𝑙𝑜𝑔𝑥 𝑑𝑦/𝑑𝑥𝑦=2/𝑥 𝑙𝑜𝑔𝑥 Step 1 Put in form 𝑑𝑦/𝑑𝑥 Py = Q xlog x 𝑑𝑦/𝑑𝑥 y = 2/𝑥 log x Dividing by x log x, 𝑑𝑦/𝑑𝑥𝑦" × " 1/(𝑥 log𝑥 ) = 2/𝑥 𝑙𝑜𝑔 𝑥" × " 1/(𝑥 log𝑥 ) 𝑑𝑦Answer to y = e^{\\tanh x} i Find \\frac{dy}{dx} ii Find \\frac{d^2y}{dx^2} By signing up, you'll get thousands of stepbystep solutions to your



If Y X 2 Sin 1 X Log X Find Dy Dx




Ex 5 5 7 Differentiate The Function Log X X X Log X
Sin(xy)= log(xy)dxd sin(xy) = dxd log(xy)cos(xy)dxd (xy) = xy1 dxd (xy)cos(xy)(1 dxdy ) = xy1 (1 dxdy )cos(xy)(1 dxdy )− xy1 (1 dxdy ) = 0(1 dxdy )(cos(xy)− xy1 ) = 0⇒ 1 dxdy = 0∴ dxdy = −1Let y = (log x) x x log x Also, let u = (log x) x and v = x log x ∴ y = u v `⇒"dy"/"dx" = "du"/"dx""dv"/"dx"` (1) u = (logx) x ⇒ log u = log (log x) x ⇒ log u = x log (log x) Differentiating both sides with respect to x, we obtainSo you really need to do a bit more work if you want to use the chain rule Basically, you need to start over, and find the derivative of f (x) = x^u, where u is some function of x, and you will find d/dx (x^u) = x^u (ln (x) (du/dx) u/x) So you find out, shockingly, that the




Find Dy Dx If Y Tan X Log X Cos 2 Pi 4 Maths Continuity And Differentiability Meritnation Com




If Sin X Y Log X Y Then Dy Dx Youtube
What is the lewis structure for co2?Y=log (x 2 /e 2) diff wr to x , we get dy/dx=1/ (x 2 /e 2) (2x/e 2) =2/x diff wr to x again d 2 y/dx 2 =2/x 2 Thanks & RegardsWe start with the function y = l n ( x) First use exponentiation with the base e to get rid of the log, a common manipulation with log equations, e y = x (*) Now take the derivative of each side, remembering to use the chain rule on ey, because y is a function of x d d x e y = d d x x and



Solve The Following Differential Equation X Dy Dx Y Xlogx X 0 Sarthaks Econnect Largest Online Education Community




Find Dy Dx When Y Log X Log X 6 Chegg Com
y = x log x (log x) x Let u = (log x) x, and v = x logx \(\therefore\) y = u v \(\cfrac{dy}{d\mathrm x}= \cfrac{du}{d\mathrm x}\cfrac{dv}{d\mathrm x} \)(i) u = (log x) x log u = log(log x) x log u = x log(log x) Differentiating both sides with respect to x, we get Therefore from (i), (ii), (iii), we get If x m y n = (xy) mn, prove that dy/dx = y/x Mention each and every step If y = x cot x 2x 2 – 3/x 2 x 2, find dy/dx Mention each and every step If y = (sin x) x sin 1 (x) 1/2, find dy/dx Mention each and every step find dy/dx y = (log x) x (x) log x mention each and every formula and minute details4 years ago By rearranging the give differential equation we get , dx/dy =1/y x/ (ylogy) dx/dy x/ (ylogy) =1/y Now, calculate the integrating factor (IF), e ∫1/ (ylogy) =IF Taking, logy=t (say) differentiating on both sides we get, dy=ydt IF=e ∫dt/t =e logt =t, where t=logy now, solving in linear differential equation form




Find Dy Dx If E X Y Log X Y Novocom Top



Solve X Dy Dx Y Log Y Log X 1 Studyrankersonline
Get answer If y=x^(x), "find" (dy),(dx) We have, `y=x^(2)` `therefore log y=x log x` On differentiating wrt x, we get `1/y (dy)/(dx)=x/x logY = (sin x) x ∴ log y = log (sin x) x ∴ log y = x log sin x ∴ `1/y dy/dx = x 1/sin x cos x log sin x1` ∴ `dy/dx = y x cot x log sin x ` Find dy/dx when x and y are connected by the relation if ax2 2hxy by2 2gx 2fy c = 0, then show that dy/dxdx/dy = 1 asked in Class XII Maths by nikita74 ( 1,017 points) continuity and differentiability




Find Dy Dx If Y X 1 Log X 1 Brainly In



How To Differentiate Y Xlogx Quora
Get an answer for '`y = x^(2/x)` Use logarithmic differentiation to find dy/dx' and find homework help for other Math questions at eNotesQ If y = 2^x, find dy/dx ANSWER 1) Take Logs of both sides of our equation y = 2^x So we get log (y)=log (2^x) 2) Apply relevant log rule to rhs Log rule log (a^b) = b log (a) nb the dot between b and log (a) represents x / multiply / times ) So we get log (y) = x log (2) 9 Follow 3 Aditi Jain, Meritnation Expert added an answer, on Aditi Jain answered this We have, y = log x x x log x ⇒ y = e log log x x e log x log x ⇒ y = e x log log x e log x log x ⇒ dy dx = e x log log x × d dx x log log x e log x 2 × d dx log x 2 ⇒ dy dx = log x x x × 1 log x × 1 x log log x x log x




If Y Log X X X Log X Then Dy Dx




Ex 5 5 7 Differentiate The Function Log X X X Log X
Ex 95, 9 In each of the Exercise 1 to 10 , show that the given differential equation is homogeneous and solve each of them 2 =0 Step 1 Find 2 =0 dy log 2 = y dx = log 2 = 2 log = 2 log Step 2 Putting F (x , y) = and finding F ( x, y) F (x, y) = 2 log ( , ) = 2 log = 2 log = ( , ) Thus, F (x, y) is a homogenous equation function ofHere we look at doing the same thing but using the "dy/dx" notation (also called Leibniz's notation) instead of limits We start by calling the function "y" y = f(x) 1 Add Δx When x increases by Δx, then y increases by Δy y Δy = f(x Δx) 2 Subtract the Two FormulasFind the derivative dy/dx of y=(34xx^2)/ln x Do you need a similar assignment done for you from scratch?




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




If Y Logx X Find Dy Dx Maths Limits And Derivatives Meritnation Com
Find dy/dx y = natural log of x^2 y = ln (x2) y = ln ( x 2) Differentiate both sides of the equation d dx (y) = d dx (ln(x2)) d d x ( y) = d d x ( ln ( x 2)) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps Differentiate using the chain rule, which states thatFind dy/dx of y = a^x To differentiate a function of the form y=a^x you need to use a neat little trick to rewrite a^x in the form of something you already know how to differentiate Using the fact that e^ln(x) is equal to x, y = a^x can be written as e^(ln(a)^x) Using log rules ln(a)^x can be written as xlna so now y can now be expressed as y Find #dy/dx#of #y=x^logx (log x)^x#?




Find Dy Dx If Xy Yx Log A Maths Continuity And Differentiability Meritnation Com




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 30 Derivatives Download Free Pdf
If y = tan1 a/x log (xa/xa) 1/2, prove that dy/dx = 2a 3 /(x 4 – a 4) Mention each and every step Queries asked on Sunday & after 7pm from Monday to Saturday will be answered after 12pm the next working dayFind Dy Dx If Y Log Base 7 Log X Math Continuity And Differentiability Meritnation Com For more information and source, see on this link https//wwwTherefore, for given y = tan x y=\tan x y = tan x We have d y = ( tan x) ′ d x dy= (\tan x)'\,dx d y = ( tan x) ′ d x As we know from the Table of Derivatives of Trigonometric Functions ( tan x) ′ = sec 2 x (\tan x)'=\sec ^2x ( tan x) ′ = sec 2 x Therefore, we have



Find The General Solution Of The Differential Equation Xlogx Dy Dx Y 2 X Logx Sarthaks Econnect Largest Online Education Community



What Is The Derivative Of X 2 Log X Quora
1) If x = a 1 1 g16 g167 g169 g168 g1 g185 g184 t, y = a 1 1 g14 g167 g169 g168 g1 g185 g184 t then, show that dy dx = − 1 2) If x = 4 1 2 t t , y = 3 1 1 2 2 g16 g14 g167 g169 g168 g1 g185 g184 t t then, show that dy dx = − 9 4 x y 3) If x = tlogt, y = t t then, show that dy dx − y = 0 36 Second Order Derivative Consider a Find an answer to your question if y = x log x log 5 then find dy/dx nj nj Math Secondary School answered If y = x log x log 5 then find dy/dx 1 See answer nj is waiting for your help Add your answer and earn pointsCalculus Find dy/dx y=xe^x y = xex y = x e x Differentiate both sides of the equation d dx (y) = d dx (xex) d d x ( y) = d d x ( x e x) The derivative of y y with respect to x x is y' y ′ y' y ′ Differentiate the right side of the equation Tap for more steps




Finding The Derivative Of Log X Video Lesson Transcript Study Com
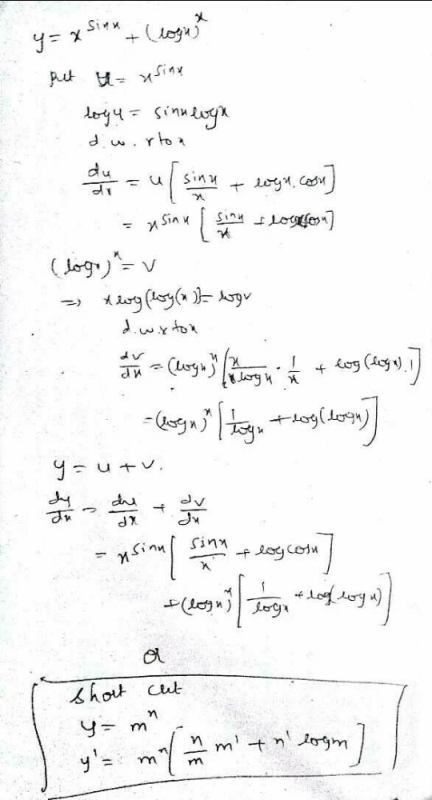



Pls Answer This It S Urgent Y X Sinx Logx X Find Dy Dx Edurev Jee Question
Calculus 1 Answer Epsilon Explanation please see the image file to explanation Answer link Related questions How do I determine the molecular shape of a molecule?যদি `x^(y)y^(x)=log a` আবিষ্কার `(dy)/(dx)` যদি `x^(y)y^(x)=log a` আবিষ্কার `(dy)/(dx)` Books Physics NCERT DC Pandey Sunil Batra HC Verma Pradeep Errorless Chemistry NCERT P Bahadur IITJEE Previous Year Narendra Awasthi MS Chauhan BiologyIf y = a cos (log x) b sin (log x) where a, b are parameters then x 2 y'' xy' = If y = a sin x b cos x, then y 2 (dy/dx) 2 is a If y = ax n1 bxn, then x 2 d 2 y/dx 2 = If y = cos1 (3 cos x 4 sin x)/5, then dy/dx = If y = cot1 (cos 2x) ½, then the value of dy / dx at x = π / 6 will be If y = e √x, then dy/dx equals




If X Ex Y Prove That Dy Dx X Y Xlogx Maths Continuity And Differentiability Meritnation Com



Q Tbn And9gcrcifas9tk9ynnvxnsymerpbvtqhsvwlu9sla5hips1tnshbunu Usqp Cau
We have qualified writers to help you We assure you an A quality paper that is free from plagiarism Order now for an Amazing Discount!Y = log (x^21) log x Now, you have to recall the derivative formula for logarithmThat is, log y = 1/y * dy dy/dx = 1/ (x^21) *derivative of (x^21) 1/x* derivative of (x)Transcribed image text Use implicit differentiation to find dy/dx and d y/dx y2x2 7 y2x2 x d'y y dx dy O A dx d2y y2x x а2у dy Ов dx У' dx2 y3 x dy yx dy Ос dx y' dx у?




Derivative Of Logarithm For Any Base Old Video Khan Academy




If Y Log X X Y Then Prove Dy Dx Log X 1 Log X 2 Brainly In
Let y = ϕ (x) = a log x Let us give a small increment h to the independent variable x Therefore, ϕ (xh) = log (xh) And dy/dx = lim ϕ (xh) ϕ (x)/h as h→0 = lim a log (xh) – a log x/h as h→0 = lim a/h log (xh)/x as h→0 = lim a/h log (1h/x) as h→0 = lim a/h log (1h/x)^ (x/h) (h/x




If Y Sqrt Logx Sqrt Logx Sqrt Logx Oo T H E N Dy Dx I S




Find Dy Dx If Y X Square Root X X Ki Power 4 Log X




What Is The Derivative Of X 2 Log X Quora




Y X Logx T H E N Dy Dx I S Y Xlogy Then Dy Dx Is



Find Dy Dx When Y X Log X Log X X Sarthaks Econnect Largest Online Education Community




If Y X Sin Logx Xlogx Prove That X 2 D 2y Dx 2 X Dy Dx 2y X Logx Youtube




Find Dy Dxof Y X Logx Log X X Socratic




Find Dy Dx When Y Cosx Logx Youtube




Log X 10 2 0 Novocom Top



1




Engineering Mathematics Notes



Find The Derivative Of Log Log Log X Stumbling Robot




12th Maths 1 Pdf Pages 101 150 Flip Pdf Download Fliphtml5




If Y X 2 X Log X Then Dy Dx Is




For The Differential Equations Find The General Solution X Dy Dx 2y X 2 Log X Mathematics Shaalaa Com




1 Find The Derivative Of Each Function A E E 7 Chegg Com




Find Dy Dx If Sin X Y Log X Y Brainly In



Find Dy Dx When X And Y Are Connected By The Relation If X Ex Y Prove That Dy Dx X Y X Log X Studyrankersonline




Rd Sharma Class 12 Maths Solutions Chapter 11 Differentiation




If Y E Log X Then Dy Dx Youtube




If X Y Y X Log A Find Dy Dx Mathematics Topperlearning Com 5d6d79xx



5 Derivative Of The Logarithmic Function



What Is The Derivation Of Log Logx Quora




Finding The Derivative Of Log X Video Lesson Transcript Study Com




Ex 9 6 7 Find General Solution X Log X Dy Dx Y 2 X Log X




What Is The Derivative Of Log Y With Respect To X Mathematics Stack Exchange



Differentiate Log X Ex W R T X Log X From Mathematics Continuity And Differentiability Class 12 Cbse




Use Logarithmic Differentiation To Find Dy Dx Y Chegg Com




If Y Logx X Then Dy Dx
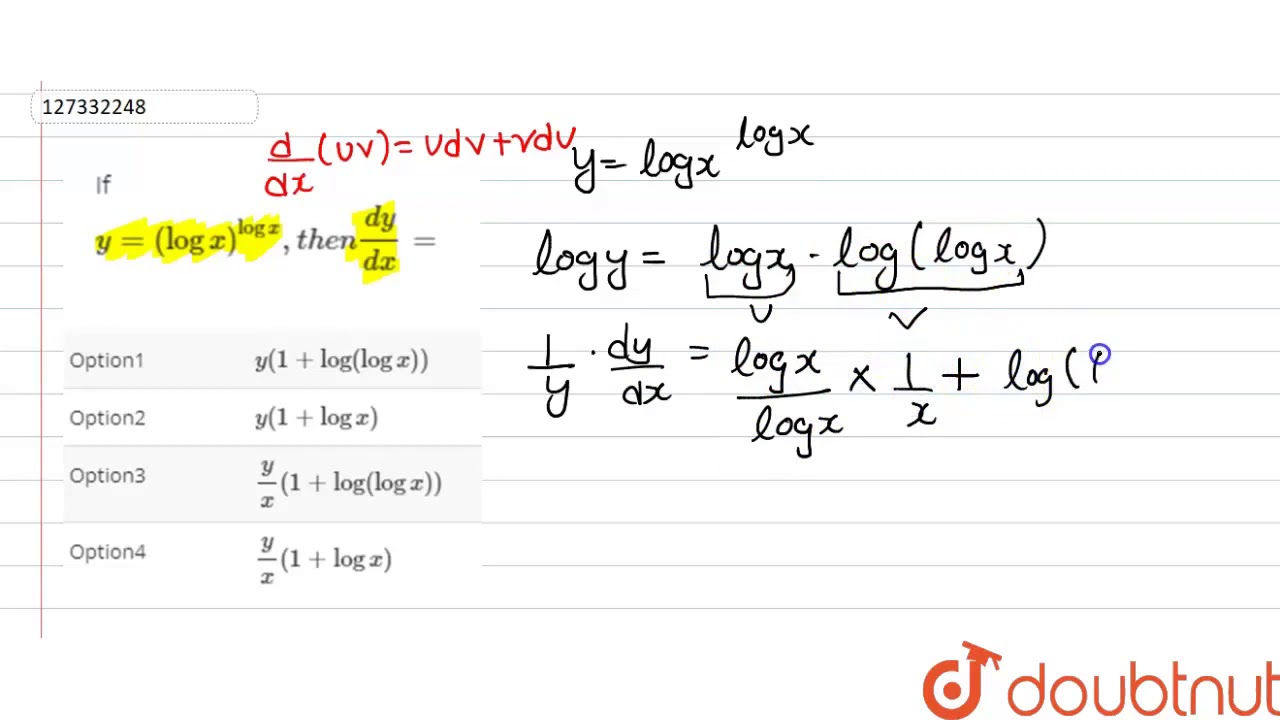



If Y Log X Logx Then Dy Dx Youtube




Ex 5 5 3 Differentiate The Function Log X Cos X Teachoo



If X Y Y X What Is Dy Dx Quora



Find The Derivative Of The Function X Sin X Log X Mathematics Topperlearning Com Wca5wyy




Y Sin X Log X Find Dy Dx Brainly In




5 Derivative Of The Logarithmic Function




If Y Log7 Log X Find Dydx




If Y E Tan X Log X Tan X Then Find Dy Dx Youtube




If Y X Logx Log Logx Then Dy Dx




If Y E Log X 5 Find D Y D X




If Y X Log X Find Dy Dx Youtube




Y Cos X Log X Find Dy Dx Scholr




Problem 2 2 Points Find Dy Dx When Y Frac Log X Gauthmath



Q Tbn And9gctkbykwijj Oieh W 6i9ywfa5m4sug9zi0ay8z2z0tdzqax3t Usqp Cau



Solve Y D Dx Xy X Sinx Logx Studyrankersonline




Ify Xlog X A Bx Then Prove That X3d2y Dx2 Xdy Dx Y 2 Brainly In




Ex 5 5 7 Differentiate The Function Log X X X Log X




Ex 5 7 9 Find Second Order Derivatives Of Log Log X



What Is The Derivative Of X Y Y X 11 Quora




X Y Dx Dy 0 Novocom Top



1




Engineering Mathematics Notes




If Y Logx Sin X Then Dy Dx




Question 4 A Implicitly Derive The Below Equation Chegg Com




Lemh105




For The Differential Equations Find The General Solution Y Log Y Dx X Dy 0 Mathematics Shaalaa Com
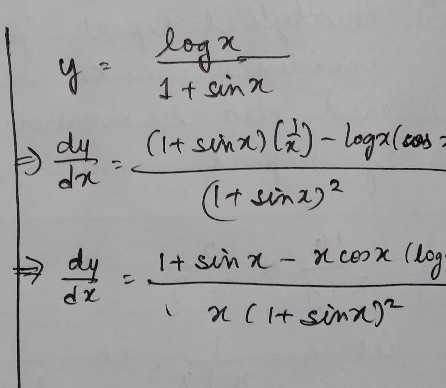



Y Logx 1 Sinx Find Dy Dx Scholr



If Math X Y Y X Math Then Math Dfrac Dy Dx Dfrac Y X Left Dfrac Y X Log Y X Y Log X Right Math Quora



Solved Differentiate Y 10 Lnx 1 Log X X 2 X 2 Find Dy Dx Forln X 2 5y 2 5 Y X 3 Analyze And Graph The Following Function Show Th Course Hero




If Y X Sin X Log X X Then Find D Y D X
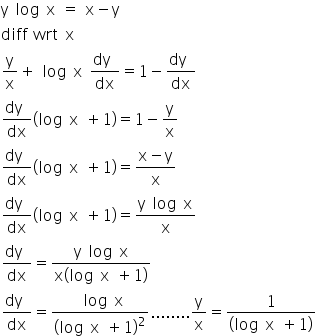



If Y Log X X Y Prove That Dy Dx Log X 1 Log X 2 Mathematics Topperlearning Com 2dolmeyy




If Y Sin X Log X Then Dy Dx




If Y X Logx Then Dy Dx Is Maths Limits And Derivatives Meritnation Com




X Dy Dx Y X Logx




If Xy Log X Y 1 Prove That Dydx Y X 2y X Y X Xy 2 X Y



How To Differentiate Y E Xlogx X 2 Quora



Solve The Linear Differential Equation Dy Dx Y X Log X Sin 2x Log X Sarthaks Econnect Largest Online Education Community



Solve The Linear Differential Equation X Dy Dx Y X Log X Sarthaks Econnect Largest Online Education Community




If Y X Log Logx Then Dy Dx Is



Www Toppr Com Ask Question Solvexlog Xdfracdydxydfrac2xlog X



Find The Integral Of 1 X Log X Stumbling Robot
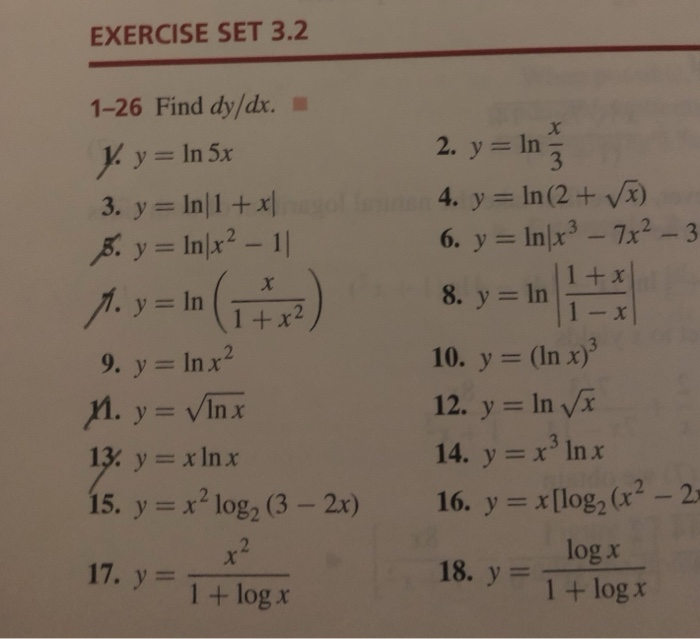



Exercise Set 3 2 1 26 Find Dy Dx 2 Y In 3 1 X 10 Chegg Com



Logarithmic Differentiation Geeksforgeeks




If Y X Logx Log Logx Then Find The Value Of Dy Dx Askiitians
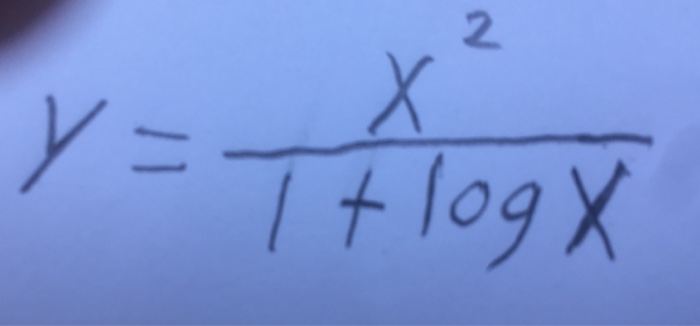



Find Dy Dx Y X 2 1 Log X Chegg Com




Differentiate X Logx Log Log X W R T X From Mathematics Continuity And Differentiability Class 12 Up Board




Dy Dx X Y 1 X Y 3 Novocom Top




Derivative Of Logₐx For Any Positive Base A 1 Video Khan Academy



Ans Man 40 12 Find Dy Dx When Y Frac Ex1 Log Gauthmath



0 件のコメント:
コメントを投稿